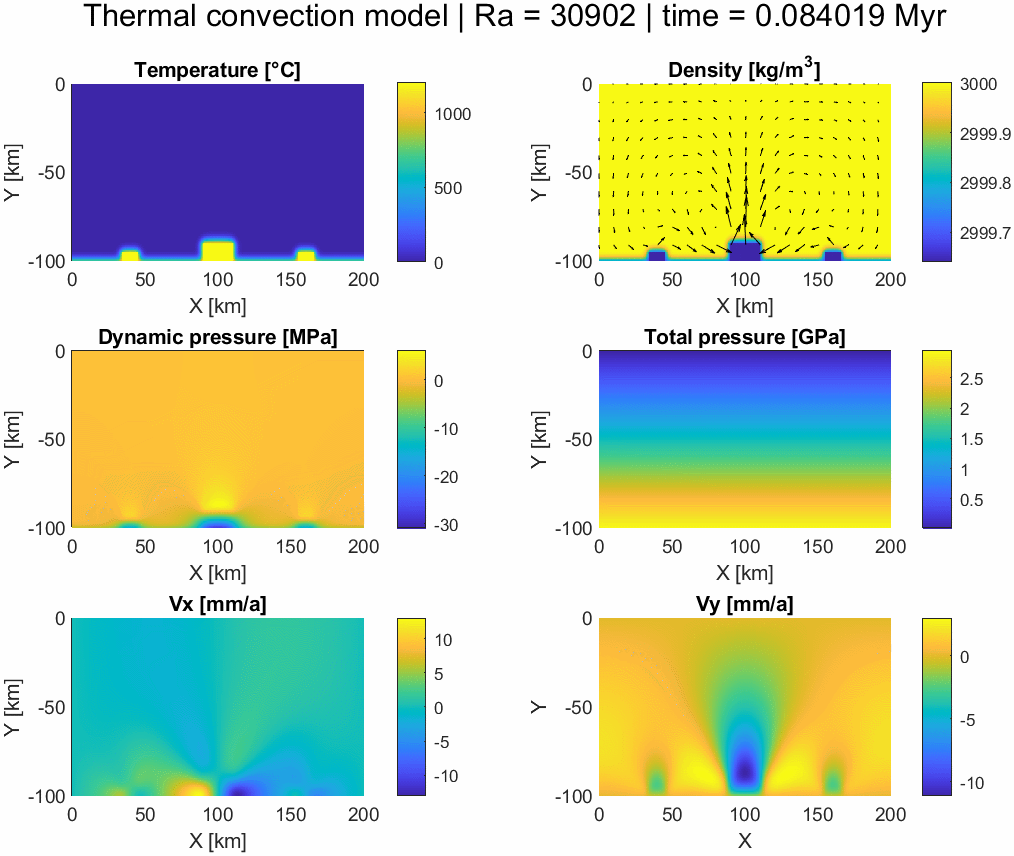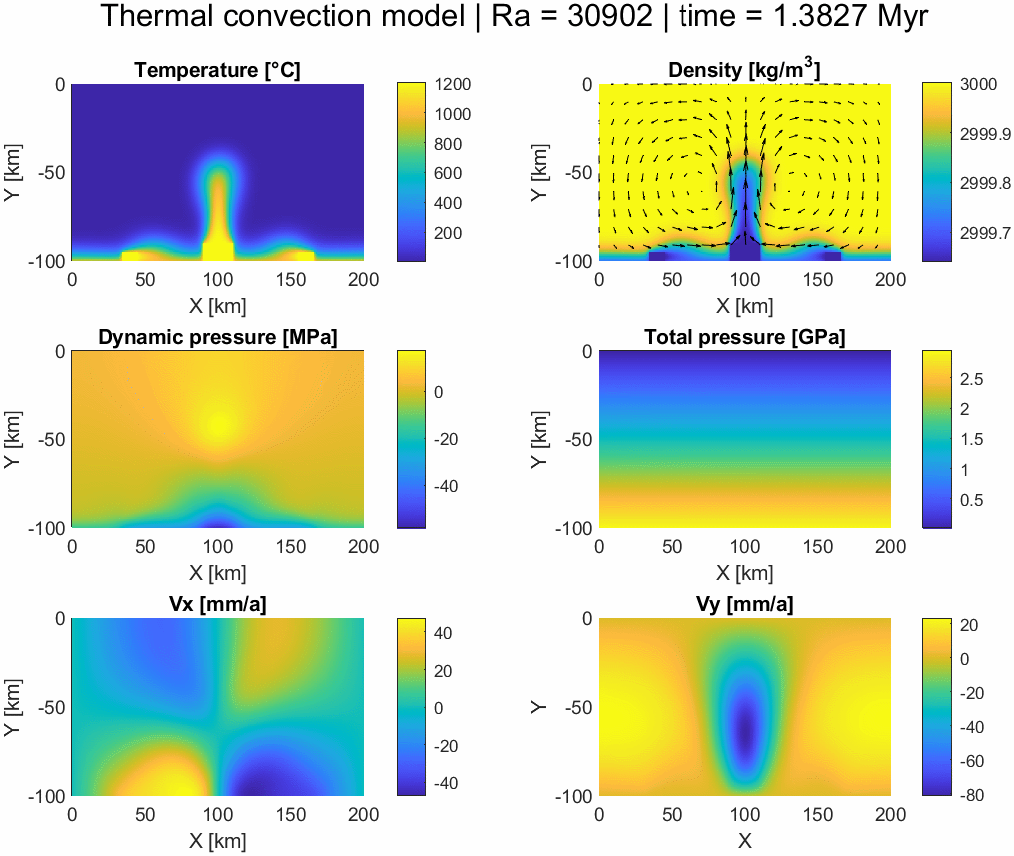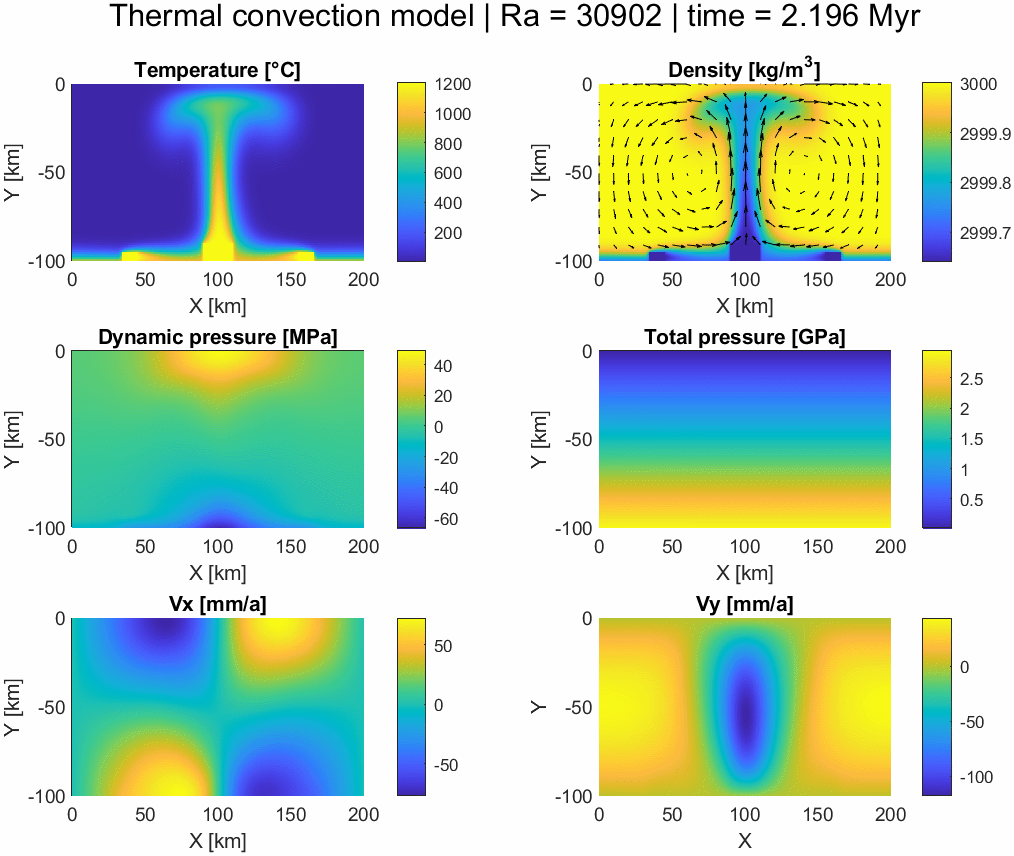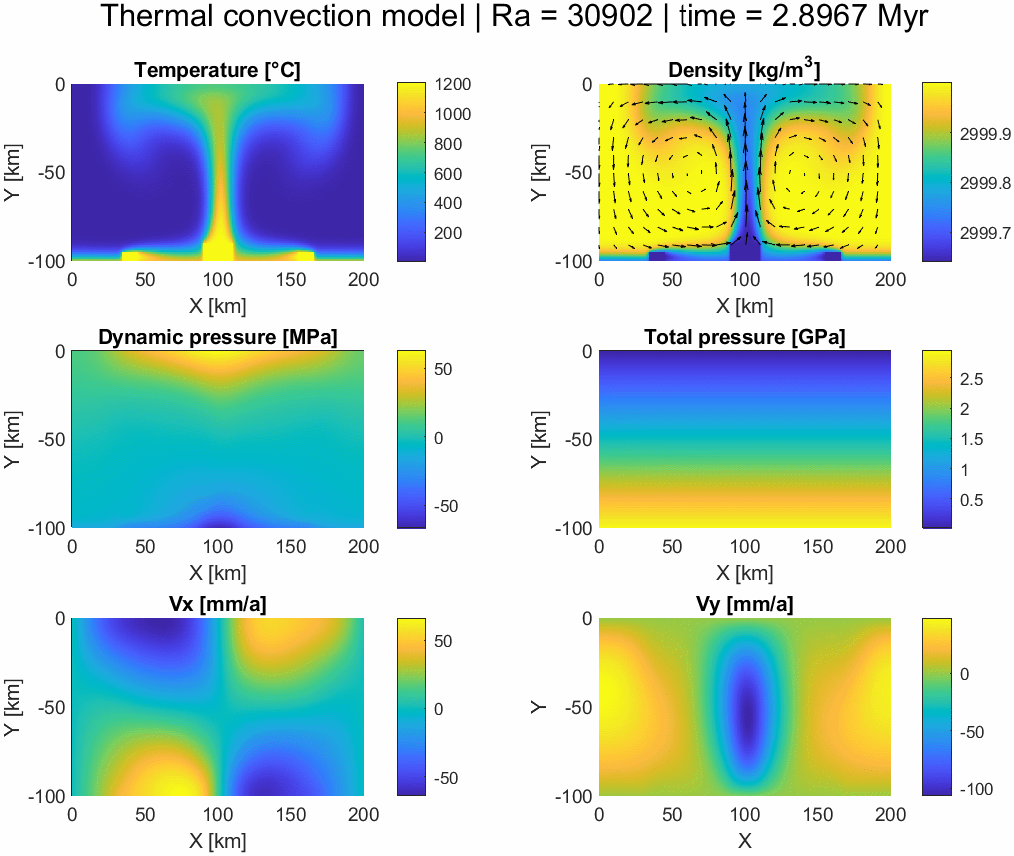
Thermomechanical convection model
An example of a numerical model based on the conservation of energy and momentum coupling the Stokes equations with thermal conduction and convection. It is solved in a non-dimensional system using an explicit finite differences scheme with the pseudotransient method (with physical time steps after convergence is reached using pseudo-time) before rescaling and plotting. The density is temperature-dependent following the Boussinesq approximation and the model assumes incompressible flow (∇⋅v = 0). Temperature is advected using a simple upwind scheme.
T1dH – 1D Temperature–Enthalpy calculations
T1dH allows to calculate Temperature diffusion in 1D using the enthalpy method, thereby enabling simulations of endo- & exothermic geological processes such as the consumption of latent heat during melting or the release of heat due the hydration. This can be coupled with other software (such as GDIFF, ZirTiDiS or KADMOS ) to calculate diffusion profiles in garnet & titanite and Ar–ages in micas and feldspar, respectively. T1dH uses an explicit finite difference scheme and is written in Matlab.

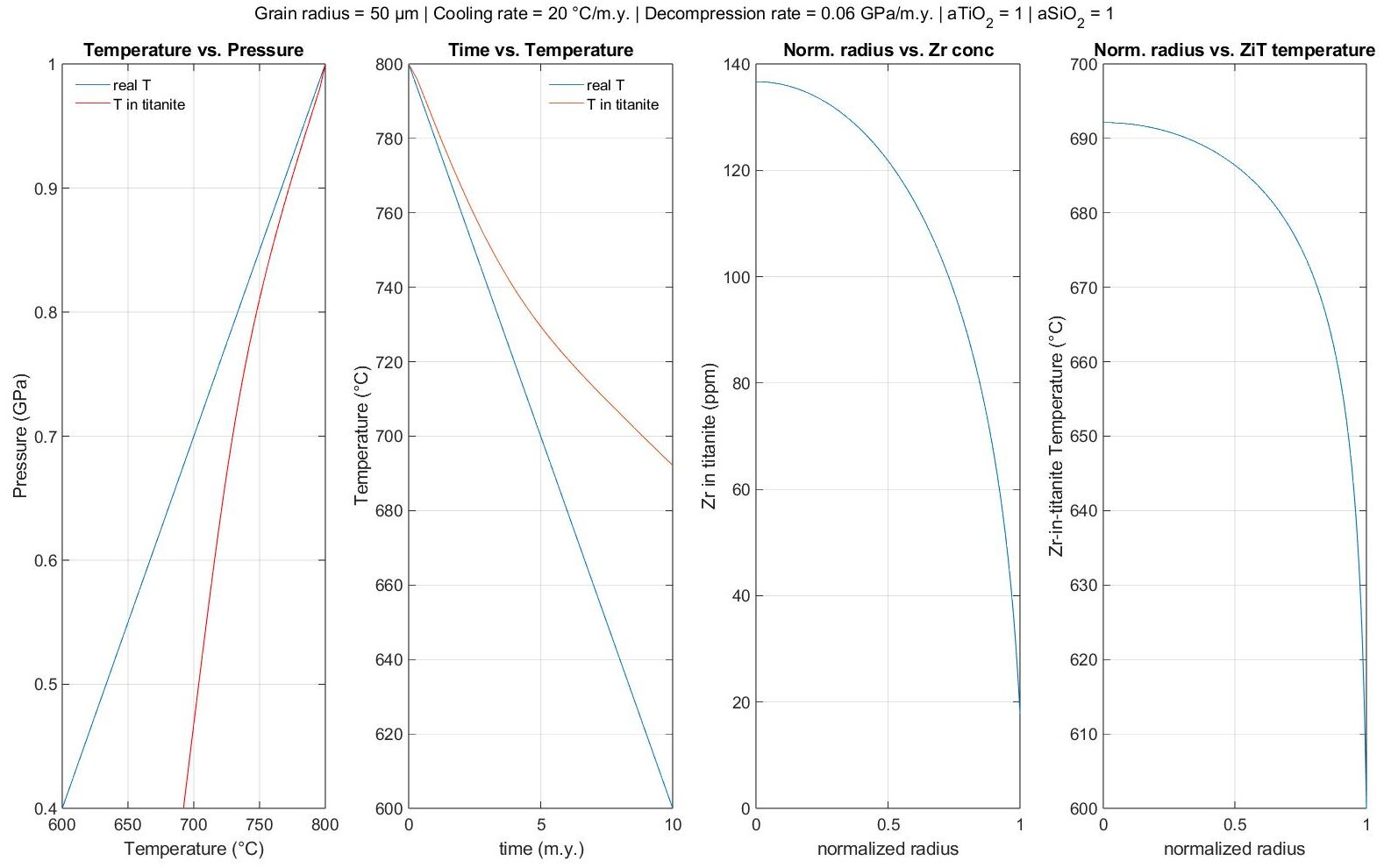
ZirTiDiS – Zirconium in Titanite Diffusion Software
This software can be used to calculate the apparent Zr-in-Titanite (ZiT) temperatures as function of a prescribed pressure–temperature–composition evolution. The required activities of silica and titania can be calculated from phase diagrams (pseudosections) and used to constrain potential cooling paths. ZirTiDiS uses an implicit finite difference scheme and is written in Matlab.
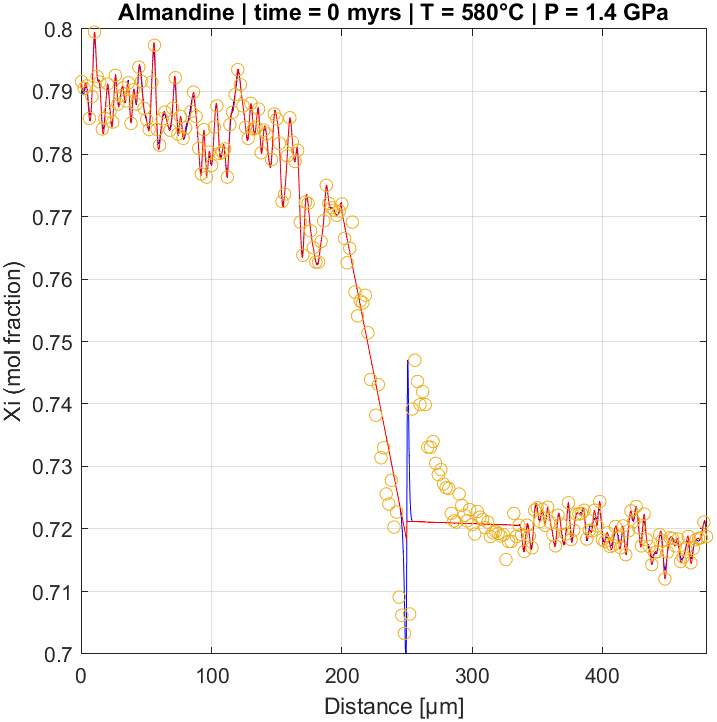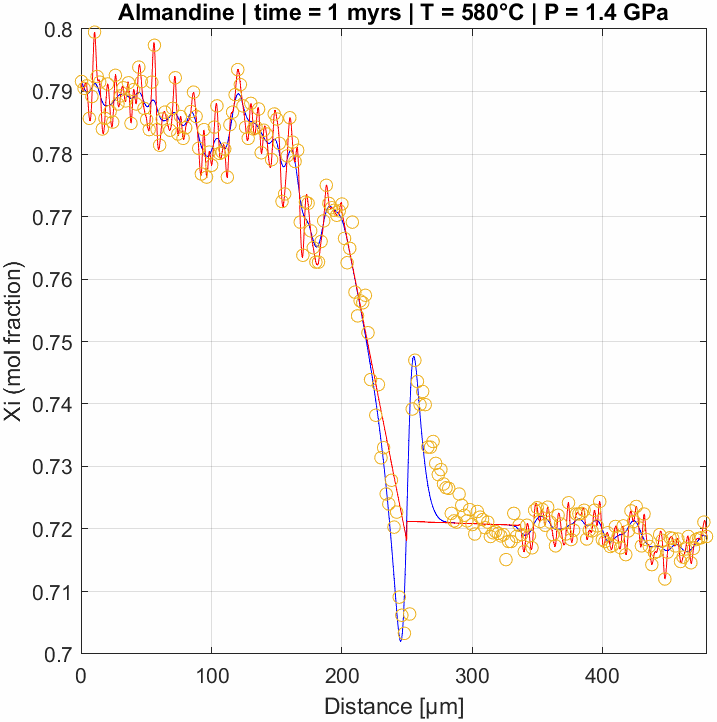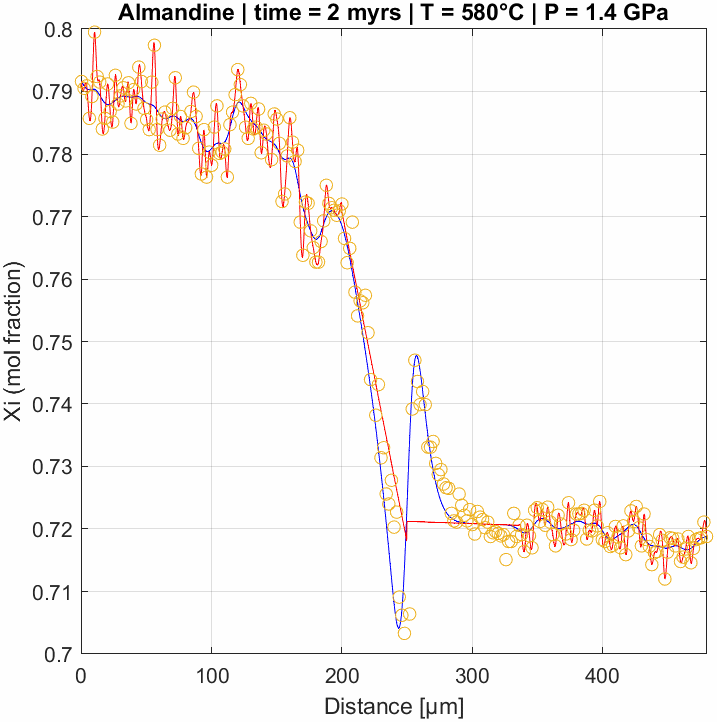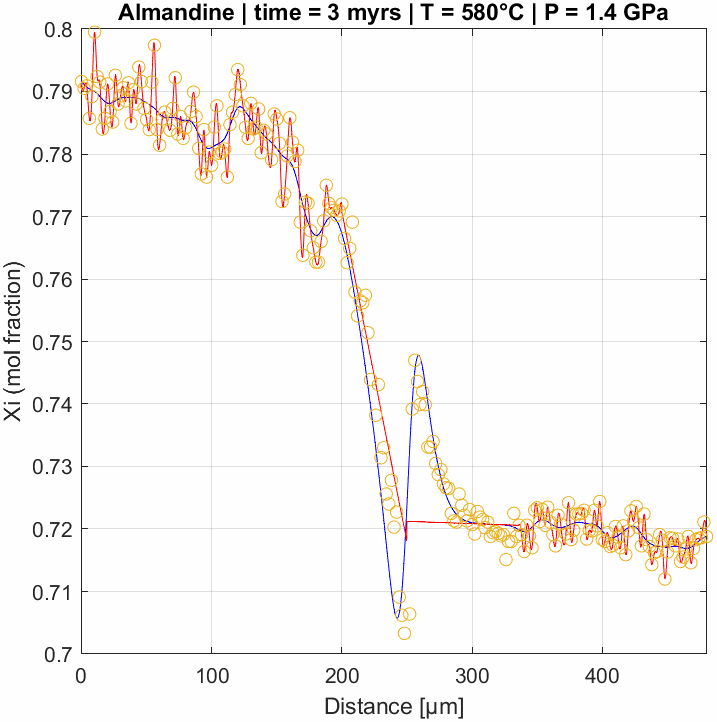
Multicomponent diffusion in garnet
Numerical model of multicomponent diffusion in garnet. This type of modelling is used to constrain the time-scales of metamorphic processes as well as rates of tectnic events. This example is particularly interesting since it nicely reproduces uphill diffusion of the almandine-component. This appears to contradict the common assumptions that diffusion flattens concentration gradients. However, it is the gradients in chemical potential that actually drive diffusion – so while these are indeed flattened during diffusion, the result may lead to this effect due to the interdependency of the diffusion coefficients (i.e., multicomponent diffusion).